Практическая реализация алгоритма
PPM
Дмитрий Шкарин
ИНСТИТУТ ДИНАМИКИ ГЕОСФЕР РАН
Москва, Ленинский проспект, 38, корпус 6
Abstract. New mechanism for PPM* data compression scheme is invented. It is demonstrated that this mechanism can provide asymptotic optimality of algorithm along with linear time complexity simultaneously. Simple procedure for adaptive escape estimation is proposed. Practical implementation of these methods is described and showed that this implementation gives best to date results at complexity comparable with widespread LZ77- and BWT-based algorithms.
Index terms: data compression, PPM algorithm, adaptive modeling.
Введение
После введения в 1984 алгоритм PPM или prediction by partial string matching стал стандартом при сравнении различных схем сжатия данных без потерь [1]. PPM последовательно строит Марковскую модель информационного источника, которая оценивает вероятность каждого символа из входной последовательности с помощью техники, называемой смешивание. Смешивание комбинирует функцию распределения частот символов из моделей различных порядков в единую функцию распределения.
Более поздняя модификация алгоритма PPM* снимает ограничение на порядок источника информации, оставляя, тем не менее, требования к памяти линейными [2].
Несмотря на то, что алгоритм PPM достигает лучших по сравнению с другими результатов, на практике он применяется достаточно редко, вследствие его большой вычислительной сложности. Данная статья посвящена построению схемы реализации алгоритма PPM, которая, сохраняя все положительные качества этого алгоритма, имеет сложность сравнимую с наиболее распространенными практическими схемами сжатия основанными на алгоритмах LZ77, LZ78, BWT [3]. По счастливому совпадению, схема ориентированная в первую очередь на малые затраты вычислительных ресурсов и простоту реализации, достигает также и наилучших из описанных на данный момент степеней сжатия.
В первой части статьи обсуждаются асимптотическое поведение алгоритма PPM и близких к нему алгоритмов и структуры данных необходимые для его реализации. В следующей части рассматривается механизм передачи информации от моделей малого порядка к моделям более высоких порядков. В третьей части рассматриваются различные методы адаптивной оценки вероятности ухода к контексту более низкого порядка. В четвертой части вводится несколько приемов увеличения степени сжатия за счет увеличения вычислительной сложности. В последней части статьи приводятся результаты сравнения предложенной схемы как с наиболее распространенными практическими реализациями алгоритмов сжатия, так и с наиболее эффективными из схем описанных в литературе.
PPM, контекстные модели и суффиксные деревья
Основная идея PPM состоит в использовании нескольких последних символов кодируемого текста для предсказания следующего символа. Строку из
k предшествующих символов будем называть контекстом 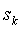 , соответствующую этому контексту модель будем называть контекстной моделью k-го порядка. В каждой модели содержится список символов, которые встречались ранее в этом контексте и счетчики частот этих символов
, соответствующую этому контексту модель будем называть контекстной моделью k-го порядка. В каждой модели содержится список символов, которые встречались ранее в этом контексте и счетчики частот этих символов 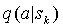 , используя которые можно найти оценку вероятности символа a в контексте
, используя которые можно найти оценку вероятности символа a в контексте 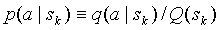 , где
, где  - сумма значений всех счетчиков частот, esc - специальный символ ухода на модель меньшего порядка,
- сумма значений всех счетчиков частот, esc - специальный символ ухода на модель меньшего порядка, 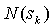 - число символов видимых в контексте. Таким образом, каждая модель хранит независимое распределение вероятностей символов, далее функции распределения вероятностей символов комбинируются в единую функцию распределения с помощью символов ухода, и любой входной символ может быть однозначно закодирован, если модель наименьшего порядка, обозначим ее
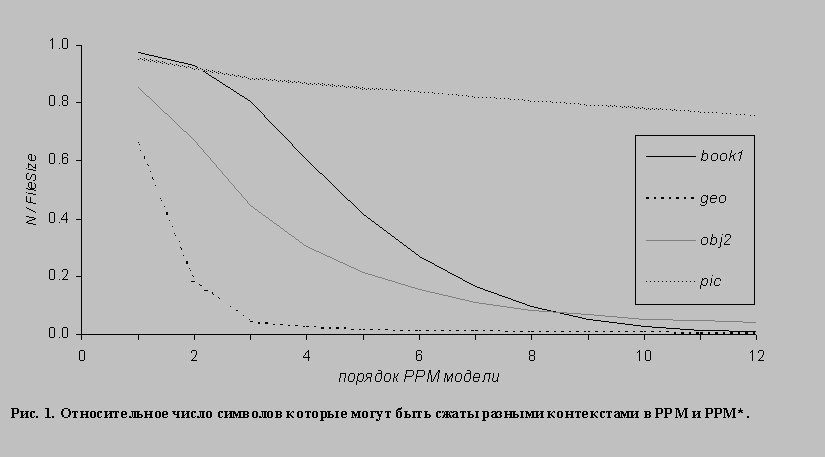
- число символов видимых в контексте. Таким образом, каждая модель хранит независимое распределение вероятностей символов, далее функции распределения вероятностей символов комбинируются в единую функцию распределения с помощью символов ухода, и любой входной символ может быть однозначно закодирован, если модель наименьшего порядка, обозначим ее 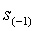 , содержит все символы входного алфавита.
, содержит все символы входного алфавита.
Наиболее удобной структурой данных для реализации PPM-алгоритма являются суффиксные деревья [4], при этом контексту соответствует узел дерева, а счетчики частот символов хранятся в структурах перехода дерева.
1.1. Ограниченные и неограниченные контекстные модели
Кратко описанный выше метод PPM имеет одно ограничение - он предполагает, что порядок источника информации заранее известен, на практике это, как правило, не так. Поэтому в работе [2] был предложен метод, снимающий это ограничение. Будем называть такой подход PPM* и соответствующие ему контекстные модели - контекстно-неограниченными.
В общем случае, если может быть использован контекст любой длины из обработанного текста, поведение модели будет нелинейным по памяти и времени выполнения, поэтому необходимо наложить некоторые разумные ограничения на выбор контекстов. Будем называть контекст бинарным, если он способен выдавать только два предсказания - либо символ, либо уход на родительский контекст. Тогда процедуру начального выбора контекста для кодирования текущего символа можно сформулировать следующим образом - если контекст максимальной длины не является бинарным, то выбираем его, в противном случае выбираем бинарный контекст минимальной длины. Далее кодирование происходит точно также как и кодирование в контекстно-ограниченных моделях. Такая реализация PPM* может быть сделана линейной по времени и памяти.
Суффиксные деревья являются наиболее удобной структурой и для реализации модели PPM*, однако необходимость поддерживать контексты неограниченной длины требует существенной реорганизации структуры дерева и введения дополнительных полей данных, а также резко уменьшает скорость работы реализации алгоритма. Например, одна из наиболее экономичных по требованиям к памяти реализаций PPM*, описанная в работе [5]
, требует 8 машинных слов на структуру небинарного контекста, 6 машинных слов на структуру бинарного контекста и 6 машинных слов на структуру перехода в небинарном контексте. Здесь учитываются также и затраты памяти на счетчики, необходимые для кодирования. Для сравнения, реализация контекстно-ограниченной модели, которая будет построена в этой статье, требует 4 машинных слова на структуру небинарного контекста, 5 машинных слов на структуру бинарного контекста и 3 машинных слова на структуру перехода в небинарном контексте. На 32-разрядных машинах эти структуры можно разместить в 3, 3 и 1.5 машинных слова, соответственно. Таким образом, контекстно-ограниченные модели при разумном выборе порядка модели (<10) являются более экономичным решением. Далее в статье всюду предполагается, что процессорное время является более дорогим ресурсом, чем оперативная память.
 На реальных данных ограниченной длины, различие между предсказаниями которые дают PPM и PPM* невелико. На Рис. 1 приведена относительная доля символов, которые могут быть предсказаны контекстами разных порядков в моделях PPM и PPM* для некоторых файлов из Calgary Corpus. Как видно, при выборе порядка модели 6 и выше, число таких символов мало и можно рассматривать модель PPM как весьма точную аппроксимацию модели PPM*. Поведение файла pic противоречит такому предположению, однако на самом деле, этот файл содержит двумерные данные и плохо соответствует парадигме “universal data compression”. В силу этого предположения, мы не будем проводить особо строгих различий между PPM и PPM* и будем применять выводы полученные для контекстно-неограниченной модели к построению реализации контекстно-ограниченной модели и наоборот, применять данные полученные с помощью этой реализации к пониманию поведения PPM*.
На реальных данных ограниченной длины, различие между предсказаниями которые дают PPM и PPM* невелико. На Рис. 1 приведена относительная доля символов, которые могут быть предсказаны контекстами разных порядков в моделях PPM и PPM* для некоторых файлов из Calgary Corpus. Как видно, при выборе порядка модели 6 и выше, число таких символов мало и можно рассматривать модель PPM как весьма точную аппроксимацию модели PPM*. Поведение файла pic противоречит такому предположению, однако на самом деле, этот файл содержит двумерные данные и плохо соответствует парадигме “universal data compression”. В силу этого предположения, мы не будем проводить особо строгих различий между PPM и PPM* и будем применять выводы полученные для контекстно-неограниченной модели к построению реализации контекстно-ограниченной модели и наоборот, применять данные полученные с помощью этой реализации к пониманию поведения PPM*.
- Асимптотическое поведение неограниченных контекстных моделей
Метод PPM* требует для своей реализации использования суффиксного дерева и счетчиков частот, расположенных в узлах дерева и структурах перехода. Число этих узлов и структур перехода пропорционально длине обработанной строки
N, таким образом, общие требования к памяти составляют O(N) (см., например, [5]).
PPM-сжатие одного символа можно рассматривать как описание пути от текущего активного состояния модели к следующему активному состоянию модели. Для того, чтобы описать этот путь, необходимо пройти вдоль него, записывая на каждой развилке соответствующие коды в выходной поток. Однако точно такой же путь необходимо проделать при построении суффиксного дерева, таким образом, сложность метода PPM* определяется процедурой построения суффиксного дерева. Описание построения суффиксного дерева с линейной сложностью можно найти в работах [6] или [7]. Итак, сложность построения модели PPM* равна
O(N).
Рассмотрим теперь развитие PPM* модели в динамике. Модель стартует с пустого дерева, затем в ней появляются короткие контексты, затем более длинные, которые закрывают более короткие. Такое явление, когда весь кодируемый текст или часть его обрабатываются в контекстах высоких порядков без использования информации, сохраненной в родительских контекстах, будем называть маскировкой родительских контекстов. Если часть собранной информации не используется, то возможно алгоритм асимптотически неоптимален. Маскировка родительских контекстов не является проблемой для контекстно-ограниченных моделей (модель ограниченна => число замаскированных контекстов ограниченно => объем потерянной информации ограничен), однако это становится проблемой для
PPM* моделей, которые теряют информацию с той же скоростью, что и получают ее от информационного источника. В качестве примера можно рассмотреть оригинальный PPM* и источник нулевого порядка с равномерным распределением символов в контексте: на каждом шаге алгоритма с практически единичной вероятностью будет создаваться новый контекст, и статистика в контекстах высокого порядка всегда будет оставаться субоптимальной. Таким образом, без принятия специальных мер, PPM* является асимптотически неоптимальным.
Известны два хорошо проработанных подхода к устранению этого недостатка:
- учет информации, сохраненной в родительских контекстах, с некоторым весом при оценке вероятности следующего символа (взвешивание);
- обращение к родительским контекстам в некоторых, “сомнительных” случаях (для краткости будем называть такой подход LOE, local order estimation);
Единственным известным автору, успешным представителем первого подхода является метод CTW [8]. Недостатком этого метода является то, что он принципиально работает только с бинарным алфавитом и объединение битов в символы выглядит достаточно искусственным.
Представители второго подхода более многочисленны, среди них и доказано оптимальные, бит-ориентированные алгоритмы CONTEXT [9] и WLZ [10], и более практичные
, байт-ориентированные FSMX-кодеры S. Bunton [5] и PPMZ-кодеры C. Bloom [11]. Недостатком этого подхода является то, что при кодировании символа механизм LOE может не использовать наиболее актуальную информацию, хранящуюся в контекстах старшего порядка.
Строго говоря, бит-ориентированные алгоритмы CTW, CONTEXT и WLZ не относятся к классу PPM алгоритмов, т.к. они не производят PPM смешивания и упоминаются здесь только для общности рассмотрения.
Оба этих подхода сканируют дерево контекстов в глубину, таким образом, их сложность составляет
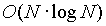 .
.
Итак, мы имеем некую дилемму: с одной стороны, алгоритм PPM* может быть реализован с линейной сложностью, но такая реализация будет асимптотически неоптимальной, с другой стороны, существуют асимптотически оптимальные реализации, но их сложность нелинейна.
2. Механизм наследования информации
Все “неприятности” происходят из-за того, что мы теряем информацию, собранную в родительских контекстах, поэтому, если мы научимся передавать эту информацию дочерним контекстам, то при правильном выборе веса с которым учитывается переданная информация, такая схема будет асимптотически оптимальной. Будем называть этот процесс наследованием информации и, соответственно, механизм его обеспечивающий - механизмом наследования информации. Следует отметить, что похожий механизм рассматривался в работе [5], там он назывался inherited frequencies, однако его значение было недооценено и асимптотическое поведение модели обеспечивалось механизмом LOE. Очевидно, что если мы будем передавать информацию только при создании новых контекстов либо при добавлении к существующим контекстам новых структур перехода, то сложность модели останется порядка O(N). При таком подходе, различные способы реализации механизма наследования информации эквивалентны введению различных функций f(…) инициализирующих начальные значения счетчиков частот символов
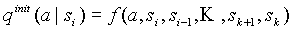 , (2.1)
, (2.1)
где
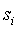 - контекст, к которому добавляется новый символ a,
- контекст, к которому добавляется новый символ a,  - контекст, который реально обработал символ a, (k < i). Теперь необходимо показать, что этот механизм способен порождать асимптотически оптимальные решения.
- контекст, который реально обработал символ a, (k < i). Теперь необходимо показать, что этот механизм способен порождать асимптотически оптимальные решения.
2.1. Пример асимптотически оптимального решения
Пусть задан источник информации порядка
N. Инициализируем в модели минус первого порядка 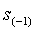 , счетчики частот символов и счетчик искейпов единицами. Будем рассматривать процедуры создания нового контекста и добавления к существующему контексту новой структуры перехода раздельно. Введем обозначения:
, счетчики частот символов и счетчик искейпов единицами. Будем рассматривать процедуры создания нового контекста и добавления к существующему контексту новой структуры перехода раздельно. Введем обозначения: 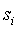 - новый контекст, a – первый символ в контексте
- новый контекст, a – первый символ в контексте 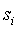 ,
,  - контекст, который реально обработал символ a, (k < i). Определим функцию передачи информации новому контексту следующим образом:
- контекст, который реально обработал символ a, (k < i). Определим функцию передачи информации новому контексту следующим образом:
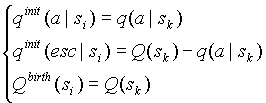 , (2.2-1)
, (2.2-1)
где
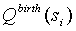 - переменная, которая будет использована далее. Будем добавлять новый символ к уже существующему контексту
- переменная, которая будет использована далее. Будем добавлять новый символ к уже существующему контексту 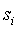 по следующему правилу:
по следующему правилу:
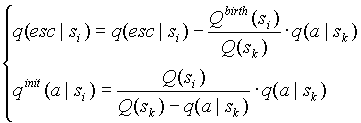 (2.2-2)
(2.2-2)
Нетрудно заметить, что функция передачи информации строится таким образом, что начальная оценка вероятности символа в контексте
 и вероятность ухода равна сумме вероятностей всех символов отсутствующих в контексте. При каждом создании нового дочернего контекста начальная масса распределения все время увеличивается, и статистические выбросы оказывают все меньшее влияние. Оценки вероятностей символов будут меняться только в контекстах длиной
и вероятность ухода равна сумме вероятностей всех символов отсутствующих в контексте. При каждом создании нового дочернего контекста начальная масса распределения все время увеличивается, и статистические выбросы оказывают все меньшее влияние. Оценки вероятностей символов будут меняться только в контекстах длиной 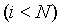 , для контекстов
, для контекстов 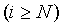 изменения функции распределения сведутся только улучшению точности представления статистики.
изменения функции распределения сведутся только улучшению точности представления статистики.
2.2. Практическая реализация механизма наследования информации
Описанный выше пример обеспечивает асимптотическую оптимальность модели, но не является практичным из-за того, что он учитывает статистику менее специализированных родительских контекстов с тем же весом, что и более точную статистику в дочерних контекстах, такой алгоритм будет плохо работать на реальных данных конечной длины. Поэтому в этом пункте рассматривается более практичное решение, хотя это решение будет асимптотически неоптимальным.
Пусть, как и в п.2.1,
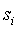 - новый контекст, a – первый символ в контексте
- новый контекст, a – первый символ в контексте 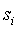 ,
,  - контекст, который реально обработал символ a, (k < i). Локально в данной точке наиболее оптимальным было бы сразу использовать модель порядка k, т.е. снизить высоту дерева до k. Такая редукция производится только локально, и влияние других потомков
- контекст, который реально обработал символ a, (k < i). Локально в данной точке наиболее оптимальным было бы сразу использовать модель порядка k, т.е. снизить высоту дерева до k. Такая редукция производится только локально, и влияние других потомков 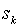 не учитывается. Для оценки вероятности символа a получаем:
не учитывается. Для оценки вероятности символа a получаем:
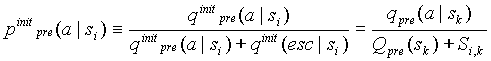 , (2.3-1)
, (2.3-1)
где
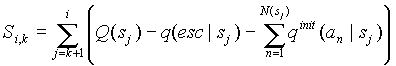 - статистика, накопленная в контекстах
- статистика, накопленная в контекстах 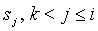 и
и  - частота символа a до обновления статистики в контексте
- частота символа a до обновления статистики в контексте 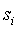 символом a. Аналогично, при добавлении нового символа в контекст
символом a. Аналогично, при добавлении нового символа в контекст 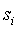 , получаем:
, получаем:
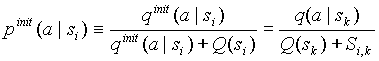 , (2.3-2)
, (2.3-2)
здесь используется статистика, уже обновленная символом
a.
Формулы (2.3-1) - (2.3-2) достаточно сложны для вычисления и требуют введения дополнительной переменной, содержащей сумму начальных значений всех счетчиков в контексте, в каждую структуру контекста, что неприемлемо для наших целей. Заметим, что, как правило, искейп
происходит на родительский контекст, т.е. 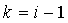 , если это не так, то статистика, накопленная в промежуточных контекстах, мала, и эти контексты оказались плохими предикторами для символа a. Поэтому не будем учитывать все промежуточные контексты
, если это не так, то статистика, накопленная в промежуточных контекстах, мала, и эти контексты оказались плохими предикторами для символа a. Поэтому не будем учитывать все промежуточные контексты 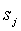 в сумме
в сумме 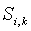 . При создании контекста, оценим начальное значение счетчика искейпов
. При создании контекста, оценим начальное значение счетчика искейпов 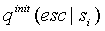 по методу C или D, при добавлении символа в контекст, заменим
по методу C или D, при добавлении символа в контекст, заменим 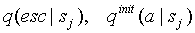 их оценкой по методу D. Используя эти упрощения в формулах (2.3-1) - (2.3-2), для начальных значений счетчиков частот символов получим для нового контекста:
их оценкой по методу D. Используя эти упрощения в формулах (2.3-1) - (2.3-2), для начальных значений счетчиков частот символов получим для нового контекста:
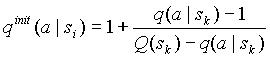 (2.4-1)
(2.4-1)
и при добавлении символа в старый контекст:
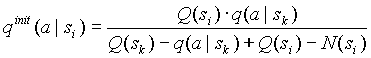 (2.4-2)
(2.4-2)
Полученные формулы достаточно просты для применения и производительность модели построенной на упрощенных формулах (2.4), в среднем, не отличается от производительности модели построенной на более строгих формулах (2.3).
Необходимым условием асимптотической оптимальности является нарастание начальной массы распределения для исключения влияния статистических выбросов на оценки вероятностей. В формулах (2.4) начальная масса распределения не зависит от порядка создаваемого контекста, поэтому такое решение будет асимптотически неоптимальным для модели PPM*, но оно вполне приемлемо для контекстно-ограниченной модели.
2.3. Модификация "update exclusions"
В обычном PPM, родительские контексты используются только для кодирования тех символов, которые не могут быть закодированы контекстами высокого порядка. При добавлении к стандартной схеме механизма наследования информации, их роль повышается - теперь они также служат шаблоном, по которому строятся контексты-потомки. В силу этого, становится более важной точность и скорость адаптации собираемой статистики в родительских контекстах. Стандартный механизм
update exclusions не обеспечивает необходимой точности и скорости адаптации, с другой стороны, full updates по-прежнему работают неудовлетворительно.
Внесем следующее изменение в стандартные
update exclusions - наряду с обновлением статистики в контексте который предсказал символ a, будем также обновлять статистику этим символом и в родительском контексте, но с весом 1/2. При update exclusions, функция распределения в родительском контексте приблизительно равна взвешенной сумме распределений в дочерних контекстах, с весами пропорциональными ширине распределения дочерних контекстов. Для того чтобы сохранить это свойство, будем отключать обновление родительского контекста после достижения счетчика частоты символа некоторого предельного значения. Экспериментально найдено, что предельное значение ~10 работает хорошо.
Описанный прием требует просмотра родительского контекста и может увеличивать время выполнения почти вдвое, что неприемлемо. Можно предположить, что если символ был обработан контекстом наибольшего порядка, то статистика в данной группе контекстов уже устоялась, вероятность использования родительского контекста мала и нет необходимости обновлять его статистику. При использовании этого предположения, время выполнения увеличивается всего лишь на 2-10%, в зависимости от порядка модели.
После введения механизма наследования информации и модификации
update exclusions, модели различных порядков начинают интенсивно обмениваться информацией и их уже нельзя рассматривать как независимые, как это часто делается при анализе различных PPM-схем, поэтому математическая формализация такого подхода затруднена.
Адаптивная оценка вероятности ухода
Выбор метода оценки вероятности ухода на контекст более низкого порядка слабо влияет на асимптотическое поведение контекстно-ограниченной модели, однако он важен при моделировании реальных данных, которые имеют ограниченную длину. В работе [1] было предложено два простых варианта оценки вероятности ухода (методы A и B), более успешный вариант был описан в работе [12], он носит название уход по методу C. В работе [13] предложена модификация метода C, называемая методом D, дающая несколько лучшие результаты. Все эти подходы выдвигают некоторые априорные предположения о природе сжимаемых данных, поэтому в работе [14] было предложено адаптивно оценивать вероятность ухода и в работе [11] приведена практическая схема реализации этого подхода.
Адаптивная оценка вероятности ухода реализуется с помощью построения дополнительной контекстной модели для бинарного алфавита, символами в котором являются пара “символ может быть закодирован текущим контекстом” и “уход на родительский контекст”. Для того чтобы не путать эту модель с основной моделью будем называть ее SEE (
secondary escape estimation) моделью, а контексты этой модели – SEE-контекстами. В работе [11] строится SEE модель второго порядка с достаточно громоздкой процедурой взвешивания контекстов различных порядков. Такой вычислительно сложный подход неприемлем для наших целей, и мы ограничимся построением модели первого порядка без взвешивания и без уходов к контекстам меньших порядков. Это накладывает ограничение на максимально-допустимое число различных SEE-контекстов, в противном случае, статистика собранная в каждом контексте будет недостаточной.
Вероятности ухода для бинарных контекстов, контекстов с более чем одним символом в контексте и контекстов, часть символов в которых замаскирована, зависят от существенно разных величин, поэтому мы будем рассматривать их раздельно, однако прежде, нам необходимо ввести простую структуру данных, необходимую для сбора статистики о
счетчиках ухода.
enum CONSTANTS { SUMM_SHIFT = 7, MAX_COUNT = 1 << SUMM_SHIFT };
struct PRIME_MEAN_ESTIMATOR {
int Summ, Count;
PRIME_MEAN_ESTIMATOR(int InitVal,int InitCount):
Summ(InitVal*InitCount), Count(InitCount) {}
int getMean() { return Summ/Count; }
void update(int Val) {
Summ += Val; Count++;
if (Count == MAX_COUNT) {
Summ >>= 1; Count >>= 1;
}
}
};
struct LOCO_MEAN_ESTIMATOR {
int Mean, Count, B; /* -Count < B <= 0 */
LOCO_MEAN_ESTIMATOR(int InitVal,int InitCount):
Mean(InitVal), Count(InitCount), B(-InitCount/2) {}
int getMean() { return Mean; }
void update(int Val) {
B += Val; Count++;
if (B <= -Count) {
Mean--; B += Count;
if (B <= -Count) B = -Count+1;
} else if (B > 0) {
Mean++; B -= Count;
if (B > 0) B = 0;
}
if (Count == MAX_COUNT) {
B >>= 1; Count >>= 1;
}
}
};
struct SIMPLE_MEAN_ESTIMATOR {
int Summ;
SIMPLE_MEAN_ESTIMATOR(int InitVal): Summ(InitVal << SUMM_SHIFT) {}
int getMean() {
int Mean=Summ >> SUMM_SHIFT;
Summ -= Mean; return Mean;
}
void update(int Val) { Summ += Val; }
};
Рис.
2. Различные способы адаптивной оценки среднего значения распределения.
3.1. Простой способ адаптивной оценки среднего значения распределения
Для нахождения вероятности ухода 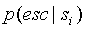 с данного контекста
с данного контекста 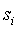 , вернее для нахождения счетчика искейпов
, вернее для нахождения счетчика искейпов 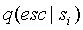 , нам понадобится адаптивный способ оценки среднего значения функции распределения. Реализация прямого способа вычисления этой оценки представлена на Рис. 2 (структура PRIME_MEAN_ESTIMATOR) в виде C++- подобного псевдокода. Алгоритм LOCO-I [15] использует более изощренный подход (структура LOCO_MEAN_ESTIMATOR), избегающий операции деления за счет добавления лишнего поля данных в структуру и двух операций условного перехода. Недостатками обоих этих подходов являются:
, нам понадобится адаптивный способ оценки среднего значения функции распределения. Реализация прямого способа вычисления этой оценки представлена на Рис. 2 (структура PRIME_MEAN_ESTIMATOR) в виде C++- подобного псевдокода. Алгоритм LOCO-I [15] использует более изощренный подход (структура LOCO_MEAN_ESTIMATOR), избегающий операции деления за счет добавления лишнего поля данных в структуру и двух операций условного перехода. Недостатками обоих этих подходов являются:
- большая вычислительная сложность (на современных процессорах цена операции условного перехода сопоставима с ценой операции деления). Для реализации PRIME_MEAN_ESTIMATOR требуется две операции сложения, одна операция деления и одна операция условного перехода. Для реализации LOCO_MEAN_ESTIMATOR требуется две операции сложения и три операции условного перехода;
- большие затраты памяти, т.к. сложные контекстные модели могут потребовать использования тысяч или даже миллионов таких структур. Для PRIME_MEAN_ESTIMATOR необходимо два машинных слова, для LOCO_MEAN_ESTIMATOR - три;
- точность представления среднего значения непостоянна, она максимальна перед операцией масштабирования и минимальна после нее;
Эти недостатки можно избежать с помощью следующего приема (структура SIMPLE_MEAN_ESTIMATOR): зафиксируем счетчик
Count, и на каждом шаге алгоритма будем добавлять к сумме Summ новое значение и вычитать среднее значение. Операцию деления можно заменить операцией сдвига, выбрав значение счетчика Count равным степени двойки. Для реализации SIMPLE_MEAN_ESTIMATOR требуется две операции сложения и одна операция арифметического сдвига, затраты памяти – одно машинное слово. Недостатком такого подхода является сильная зависимость от правильного выбора первоначального приближения InitVal в начале кодирования. Этот дефект может быть скорректирован выбором малого значения сдвига при начале кодирования и постепенным его увеличением до SUMM_SHIFT по мере набора статистики, такая корректировка почти не увеличивает сложности реализации, но требует введения в структуру SIMPLE_MEAN_ESTIMATOR двух дополнительных полей данных.
Дополнительный выигрыш в быстродействии может быть получен при кодировании бинарного алфавита, т.е. алфавита имеющего всего два символа –
‘0’ и ‘1’, при этом оценка среднего значения распределения является также и оценкой вероятности символа ‘1’. Масштабируя полный интервал вероятностей [0, 1] к числу равному степени двух, можно исключить деление в арифметическом кодере.
Предложенный способ может быть использован в различных моделирующих и статистических программах работающих с аналоговыми сигналами, и он действительно успешно используется в программе [16].
3.2. Оценка вероятности ухода с бинарного контекста
Случай бинарного контекста наиболее прост, т.к. соответствующая ему контекстная модель имеет единственный свободный параметр – сколько раз контекст 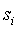 встречался в прошлом, поэтому эта величина хорошо подходит в качестве элемента SEE-контекста.
встречался в прошлом, поэтому эта величина хорошо подходит в качестве элемента SEE-контекста.
Алгоритм PPM эксплуатирует сходство родительских и дочерних контекстов, поэтому число различных символов встречавшихся в родительском контексте
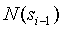 хорошо коррелирует с вероятностью ухода с дочернего контекста. Добавим число символов в родительском контексте
хорошо коррелирует с вероятностью ухода с дочернего контекста. Добавим число символов в родительском контексте 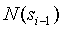 , квантизованное до трех бит к SEE-контексту.
, квантизованное до трех бит к SEE-контексту.
Эксперименты показывают, что на реальных данных блоки хорошо предсказуемых данных чередуются с блоками плохо предсказуемых данных, величина таких блоков невелика – порядка 3-5 символов, это соответствует разделению на слова и части слов в текстах на естественных языках. Для того чтобы отслеживать переключение между такими блоками, вставим в SEE-контекст вероятность появления предыдущего символа в предыдущем контексте, квантизованную до одного бита.
3
.3. Оценка вероятности ухода с небинарного контекста
Этот тип контекстов представляет собой более сложный случай – с одной стороны, такие контексты встречаются относительно редко в моделях высоких порядков и для них трудно набрать достаточную статистику, с другой стороны, простые методы оценки вероятности ухода, подобные тому, что описан в предыдущем подразделе, не дают заметного выигрыша. По этой причине, будем использовать полуадаптивный метод, выбрав в качестве начального приближения уход по методу D.
Предположим, что вероятности символов в контексте распределены по экспоненциальному закону, т.е.
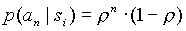
тогда, при превращении бинарного контекста в небинарный, на основе модели предыдущего пункта, можно найти основание степени
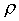 и из него найти величину счетчика уходов
и из него найти величину счетчика уходов 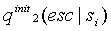 для контекста содержащего два символа. Эти вычисления можно произвести только численно, т.к. символы необязательно появляются в контексте в порядке убывания вероятности. Предположение об экспоненциальном законе распределения символов работает всегда хорошо, т.к. оно применяется для контекста содержащего всего один или два символа.
для контекста содержащего два символа. Эти вычисления можно произвести только численно, т.к. символы необязательно появляются в контексте в порядке убывания вероятности. Предположение об экспоненциальном законе распределения символов работает всегда хорошо, т.к. оно применяется для контекста содержащего всего один или два символа.
Далее значение
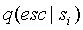 будем корректировать только при добавлении новых символов в контекст, аналогично тому, как это делается в методе D, но не для каждого добавляемого символа. Будем добавлять к счетчику
будем корректировать только при добавлении новых символов в контекст, аналогично тому, как это делается в методе D, но не для каждого добавляемого символа. Будем добавлять к счетчику 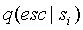 величину:
величину:
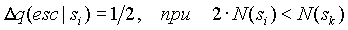 ,
,
где
N(s) - число символов в контексте s, 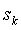 - контекст, который реально обработал текущий сжимаемый символ, (k < i). Дополнительная корректировка требуется, когда новый добавленный символ имеет малую вероятность в текущем контексте, добавим в этом случае величину:
- контекст, который реально обработал текущий сжимаемый символ, (k < i). Дополнительная корректировка требуется, когда новый добавленный символ имеет малую вероятность в текущем контексте, добавим в этом случае величину:
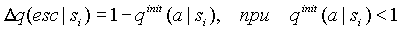
3.4. Оценка вероятности ухода с контекста с "замаскированными" символами
Для этого типа контекстов, счетчик ухода в наибольшей степени коррелирует с числом незамаскированных символов, квантизуем эту величину до 42 значений (приблизительно 5-6 бит). Далее, опять воспользуемся подобием родительских и дочерних контекстов, и будем сравнивать число незамаскированных символов в текущем контексте с числом символов в дочернем контексте и с числом символов, которые будут незамаскированы в родительском контексте, в случае если текущий контекст не сможет обработать сжимаемый символ. Это добавляет еще два бита в SEE-контекст. Наблюдается, также, корреляция счетчика ухода с отношением  , т.е. со средним значением счетчика в контексте. Эта величина квантизуется до одного бита.
, т.е. со средним значением счетчика в контексте. Эта величина квантизуется до одного бита.
Интересно отметить, что все приведенные выше способы адаптивной оценки вероятности ухода напрямую зависят только от текущего состояния модели, но не от сжимаемых данных, это позволяет надеяться, что эти методы в достаточной степени универсальны и будут работать для широкого класса входных данных.
- Дополнительные приемы повышения производительности схемы
Построенная в предыдущих двух разделах статьи модель (далее
Model1) демонстрирует результаты в среднем превосходящие все описанные ранее схемы сжатия данных без потерь, поэтому представляется интересным выяснить предельную степень сжатия, которую подобный подход способен достичь. В этом разделе мы не будем ограничивать себя требованием малой вычислительной сложности реализации. Полученную модификацию исходной схемы будем обозначать Model2.
Часть улучшений может быть получена просто путем отказа от введенных ранее упрощений. Полные формулы (2.3) оценки величины начального значения счетчика символа, полученные на основе механизма наследования информации, не дают заметного выигрыша в степени сжатия и сильно замедляют скорость работы компрессора, поэтому по-прежнему будем пользоваться упрощенными формулами (2.4). Для метода обновления статистики в родительском контексте, описанного в п.2.4,
теперь будем обновлять статистику на каждом шаге, а не только когда дочерний контекст не является контекстом максимального порядка. Для адаптивной оценки вероятности ухода, будем использовать модификацию SIMPLE_MEAN_ESTIMATOR упомянутую в п.3.1. Точность представления счетчиков частот символов повышена с 1/4 в Model1 до 1/8 в Model2. Другие улучшения требуют отдельного рассмотрения.
4.1. Улучшение оценки вероятности наиболее вероятного символа и наименее вероятных символов в контексте
Статистика, набранная в контекстах высокого порядка, является в большинстве случаев недостаточной. Другими словами, с точки зрения математической статистики, выборка не является представительной, следовательно, необходимо относиться с осторожностью к казалось
-бы вполне очевидным понятиям математической статистики, например к определению оценки вероятности символа в контексте  . Для примера рассмотрим контекст со следующим модельным распределением вероятностей символов в контексте:
. Для примера рассмотрим контекст со следующим модельным распределением вероятностей символов в контексте:
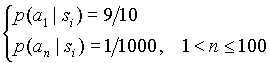 (4.1)
(4.1)
Очевидно, что контекст должен встретиться не менее девяти раз, прежде чем мы сможем сделать правдоподобную оценку
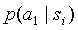 . С другой стороны, после того как контекст будет использован пятьдесят раз, вероятность того, что встретится один или более из маловероятных символов составляет 99.5%, этим символам будет присвоена оценка вероятности ~1/50, что сильно отличается от истинного распределения (4.1). Для простоты изложения, мы пренебрегаем механизмом наследования информации и вероятностью ухода на родительский контекст.
. С другой стороны, после того как контекст будет использован пятьдесят раз, вероятность того, что встретится один или более из маловероятных символов составляет 99.5%, этим символам будет присвоена оценка вероятности ~1/50, что сильно отличается от истинного распределения (4.1). Для простоты изложения, мы пренебрегаем механизмом наследования информации и вероятностью ухода на родительский контекст.
Счетчик наиболее вероятного символа можно скорректировать, используя информацию о символе из родительского контекста, если выполняются неравенства
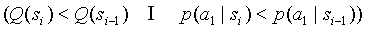 . Новое значение счетчика найдем с помощью взвешивания значения счетчика в текущем контексте и приведенного значения счетчика в родительском контексте:
. Новое значение счетчика найдем с помощью взвешивания значения счетчика в текущем контексте и приведенного значения счетчика в родительском контексте:

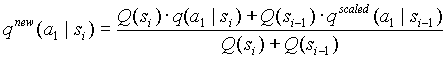 ,
,
где
 .
.
Для бинарного контекста в контекстно-ограниченной модели, эта процедура выльется просто в поиск максимального значения счетчика для всех родительских контекстов, которые являются бинарными.
Для наименее вероятных символов, счетчик просто инкрементируется на 3/4, а не на единицу:
 ,
,
где
 - среднее значение счетчика частот символов в контексте, включая искейп.
- среднее значение счетчика частот символов в контексте, включая искейп.
4.2. Отложенное добавление символов в контекст
Во втором разделе был рассмотрен механизм наследования информации, на практике он сводится к присвоению счетчику частот некоторого начального значения определяемого формулой (2.1), зависящего от контекста
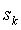 , который реально обработал символ a. При этом для простоты реализации, предполагалось, что вычисление
, который реально обработал символ a. При этом для простоты реализации, предполагалось, что вычисление 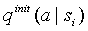 производится непосредственно после кодирования символа a. Это не является наиболее оптимальной стратегией, т.к. для контекстных моделей высоких порядков статистика в контексте
производится непосредственно после кодирования символа a. Это не является наиболее оптимальной стратегией, т.к. для контекстных моделей высоких порядков статистика в контексте 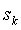 может также быть недостаточной. Представляется более выгодным, ввести некоторое специальное значение счетчика частот, показывающее, что счетчик еще не был инициализирован, и отложить инициализацию до тех пор, пока контекст
может также быть недостаточной. Представляется более выгодным, ввести некоторое специальное значение счетчика частот, показывающее, что счетчик еще не был инициализирован, и отложить инициализацию до тех пор, пока контекст 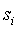 не встретится в следующий раз. Такой прием требует одного дополнительного сканирования контекста
не встретится в следующий раз. Такой прием требует одного дополнительного сканирования контекста 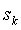 для инициализации каждого счетчика
для инициализации каждого счетчика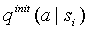 и, потому, неприемлем для Model1.
и, потому, неприемлем для Model1.
4.3 Дополнительные поля в SEE-контекстах
Элементы SEE-контекстов, введенные в третьем разделе статьи для
Model1, выбирались по признаку наименьшей вычислительной сложности, теперь мы можем добавить дополнительные поля, не связывая себя этим ограничением.
Под длинным блоком символов с длиной
L, будем понимать последовательность символов входного текста, для которой, при кодировании, ни разу не происходил уход на модели более низких порядков (не было искейпов) и L символам из нее были присвоены оценки вероятности выше, чем 1/2. Вполне вероятно, что контекстно-ограниченная модель порядка N < L, будет субоптимальной для таких блоков. Чтобы отслеживать подобную ситуацию вставим в бинарный SEE-контекст флажок, сигнализирующий о том, находится ли кодер в длинном блоке или нет.
Естественно, что текущий кодируемый символ в наибольшей степени коррелирует с предыдущим символом. В силу этого, желательно было бы ввести в SEE-контекст зависимость от последнего закодированного символа, однако вставка всего символа целиком в SEE-контекст приведет к большим расходам памяти и малой частоте появления каждого отдельного SEE-контекста, поэтому добавим в бинарный SEE-контекст и SEE-контекст для контекста с замаскированными символами только старшие два бита предыдущего символа. К бинарному SEE-контексту добавим, также, старшие два бита предсказываемого символа. Такой прием вводит зависимость SEE-контекста от порядка символов во входном алфавите, что, до некоторой степени, противоречит духу “universal data compression”. С другой стороны, он может рассматриваться как некоторая странная форма хеширования
SEE-контекстов.
Рассмотренные в этом разделе методы позволяют увеличить степень сжатия в среднем на 1.0-
2.0% ценой увеличения времени выполнения на 30-50%, поэтому они могут представлять интерес только в каких-то специальных случаях, но не для типичных задач.
5. Результаты экспериментов
Прежде чем приступить к экспериментальным сравнениям, необходимо очертить круг практических задач, для решения которых используются универсальные алгоритмы сжатия. Здесь мы не будем рассматривать задачи, для которых универсальный алгоритм сжатия инкорпорирован в какой-то другой, более общий алгоритм, например, задачу сжатия аналогового сигнала с потерями. Задача сжатия данных некоторого, заранее известного типа данных также не рассматривается. К интересующим нас задачам, например, относятся:
- тиражирование данных и программ;
- передача информации по узким каналам связи;
- резервное хранение данных (архивация, бэкап);
Критериями сравнения различных алгоритмов сжатия являются:
- степень сжатия;
- скорости кодирования и декодирования данных;
- потребности в оперативной памяти при кодировании и декодировании;
- простота реализации;
Для решения задач типа 1) крайне важна скорость декодирования, но скорость кодирования не так важна. Для задач типа 2) важна сумма времен кодирования и декодирования и для задач типа 3) более важна скорость кодирования (вполне вероятен случай, когда сохраненные данные не будут востребованы). Очевидно, что алгоритмы класса PPM слабо подходят для решения задач типа 1), т.к. они симметричны по скорости и требованиям к памяти. Для решения таких задач лучше применять алгоритмы класса LZ77. С другой стороны,
как мы увидим далее, PPM вполне подходит для решения задач типа 2) и 3).
Описанные в данной статье
Model1 и Model2 были реализованы на языке программирования C++ и публично доступны по адресу [17]. Модели Model1 соответствует исполнимый файл PPMd.exe, модели Model2 соответствует исполнимый файл PPMonstr.exe. Все эксперименты проводились на стандартном Calgary Corpus.
5.1. Сравнение затрат памяти и процессорного времени
В первом эксперименте сравнивались интегральные характеристики программной реализации
Model1 и Model2 с наиболее распространенными практическими реализациями алгоритмов LZ77 - ZIP [18] и BWT – BZIP2 [19], а также с наиболее мощной реализацией PPM* - PPMZ2 [20].
Все программы, за исключением
PPMZ2, были откомпилированы одним и тем же компилятором (Intel C v.4.0). Эксперименты проводились на компьютере PII-233(292) МГц с оперативной памятью 64 МБ, под ОС Windows98 и файловой системой FAT32. Измерение времени производилось системным таймером, каждая программа запускалась пять раз и выбиралось наименьшее время выполнения. Результаты измерения средней степени сжатия (в битах на байт), времени сжатия всего корпуса и пиковой потребности в памяти (в мегабайтах) представлены в Таблице 1.
|
Порядок модели |
Model1 |
Model2 |
|
Средний bpb |
Время, сек. |
Память, МБ |
Средний bpb |
Время, сек. |
Память, МБ |
|
2 |
2.758 |
3.24 |
0.5 |
2.763 |
4.94 |
0.6 |
|
3 |
2.369 |
3.84 |
1.3 |
2.376 |
6.04 |
1.4 |
|
4 |
2.219 |
4.56 |
2.3 |
2.221 |
7.14 |
2.4 |
|
5 |
2.168 |
5.38 |
4.2 |
2.157 |
8.35 |
4.3 |
|
6 |
2.150 |
6.26 |
8.0 |
2.129 |
9.50 |
8.1 |
|
8 |
2.134 |
7.74 |
19 |
2.106 |
11.42 |
19 |
|
10 |
2.129 |
9.00 |
34 |
2.097 |
12.02 |
34 |
|
16 |
2.123 |
* |
84 |
2.089 |
* |
84 |
|
Для сравнения |
|
ZIP –9 |
2.764 |
5.93 |
0.5 |
|
BZIP2 -8 |
2.368 |
5.87 |
6.8 |
|
PPMZ2 |
2.140 |
* |
>100 |
Таблица
1. Интегральные характеристики различных компрессоров.
* Измерение времени выполнения не производилось из-за недостатка оперативной памяти.
Из таблицы видно, что
Model1 обеспечивает широкий круг возможностей. При малых порядках моделирования (2-3), она дает степень сжатия сравнимую с ZIP и BZIP2, при более высокой скорости выполнения и меньших затратах памяти чем у BZIP2. При средних порядках моделирования (4-6), она дает заметно лучшую степень сжатия, затраты времени и памяти, при этом, остаются сравнимыми с BZIP2. И наконец, при высоких порядках моделирования (8-16), Model1 превосходит лучшую из описанных до сих пор программу PPMZ2 по степени сжатия, быстродействию и требованиям к памяти.
Model2, как правило, дает несколько лучший результат, чем Model1. Исключением являются только малые порядки моделирования (2-4). Это объясняется тем что, при малых порядках модели, число бинарных контекстов невелико и статистика в них не успевает устояться, т.к. Model2 использует более широкий SEE-контекст, то на ней это сказывается сильнее.
5.2. Сравнение производительности
Во втором эксперименте более подробно сравнивается производительность
Model1 и Model2 с наилучшими из схем сжатия описанными в литературе. В Таблице 2 представлены результаты работы следующих схем сжатия: реализации метода CTW [21], ассоциативного кодера Г. Буяновского (ACB) [22], лучшего из описанных S. Bunton FSMX-кодеров [5], PPMZ2 by C. Bloom [20]. В предпоследней и последней колонках даны результаты Model1 и Model2 для порядка моделирования 16. Необходимо отметить, что реализация [21] метода CTW использует разбиение символов на биты специально оптимизированное для английских текстов, таким образом, она не является универсальным компрессором.
|
Файл |
CTW |
ACB |
FSMX |
PPMZ2 |
Model1 |
Model2 |
|
bib |
1.782 |
1.935 |
1.786 |
1.717 |
1.751 |
1.712 |
|
book1 |
2.158 |
2.317 |
2.184 |
2.195 |
2.224 |
2.174 |
|
book2 |
1.869 |
1.936 |
1.862 |
1.846 |
1.861 |
1.816 |
|
geo |
4.608 |
4.555 |
4.458 |
4.576 |
4.362 |
4.322 |
|
news |
2.322 |
2.317 |
2.285 |
2.205 |
2.225 |
2.175 |
|
obj1 |
3.814 |
3.498 |
3.678 |
3.661 |
3.547 |
3.540 |
|
obj2 |
2.473 |
2.201 |
2.283 |
2.241 |
2.186 |
2.160 |
|
paper1 |
2.247 |
2.343 |
2.250 |
2.214 |
2.210 |
2.173 |
|
paper2 |
2.190 |
2.337 |
2.213 |
2.185 |
2.208 |
2.158 |
|
pic |
0.800 |
0.745 |
0.781 |
0.751 |
0.759 |
0.749 |
|
progc |
2.330 |
2.332 |
2.291 |
2.258 |
2.223 |
2.189 |
|
progl |
1.595 |
1.505 |
1.545 |
1.445 |
1.461 |
1.423 |
|
progp |
1.636 |
1.502 |
1.531 |
1.450 |
1.469 |
1.439 |
|
trans |
1.394 |
1.293 |
1.325 |
1.214 |
1.238 |
1.210 |
|
Средний bpb |
2.230 |
2.201 |
2.177 |
2.140 |
2.123 |
2.089 |
Таблица 2. Производительность различных схем сжатия.
Model2 дает лучшие результаты на большинстве файлов, исключением являются файлы book1, obj1 и pic. На файле book1, реализация CTW [21] дает лучшие результаты т.к. она специально оптимизирована под подобный тип данных. Интересно отметить, что на других англоязычных текстовых файлах – bib, book2, news, paper1, paper2, она не дает столь впечатляющих результатов. Программа ACB использует бит-ориентированный метод сжатия, поэтому она набирает статистику примерно в восемь раз быстрее, чем байт-ориентированные программы. Это дает ей преимущество на маленьких файлах, что видно на примере файла obj1, который является самым коротким в Calgary Corpus. В файле pic записано изображение с глубиной цвета 1 бит, естественно, такие данные лучше всего моделируются бит-ориентированными методами, например ACB.
Заключение
В данной статье был описан новый базовый механизм PPM, который назван наследованием информации. Было продемонстрировано, что этот механизм способен обеспечить и линейную сложность алгоритма и асимптотическую оптимальность одновременно. Была описана простая программная реализация механизма наследования информации. Также, рассмотрен вопрос адаптивной оценки вероятности ухода на контекст более низкого порядка и предложены простые способы нахождения этой оценки. Показано, что реализации алгоритма PPM могут быть весьма практичными и достигать скоростей сжатия и требований к памяти характерных для алгоритмов LZ77 и
BWT.
Литература
[1] Cleary, J.G. and Witten, I.H. (1984) Data compression using adaptive coding and partial string matching. IEEE Transactions on Communications, 32(4):396–402.
[2] Cleary, J.G., Teahan, W.J. and Witten, I.H. (1995) Unbounded length contexts for PPM. In J.A. Storer and M. Cohn, editors, Proceedings DCC’95. IEEE Computer Society Press.
[3] Moffat, A., Bell, T.C. and Witten I.H. (1995) Lossless Compression for Text and Images. International Journal of High Speed Electronics and Systems, 8(1):179-231.
[4] Crochemore, M. and Rytter, W. (1994) Text Algorithms. Oxford University Press, Oxford.
1994.
[5] Bunton, S. (1996) On-Line Stochastic Processes in Data Compression. PhD thesis, University of Washington.
[6] Ukkonen, E. (1995) On-line construction of suffix trees. Algorithmica 14(3):249-260.
[7] Larsson, J.N. (1996) Extended application of suffix trees to data compression. Proceedings of the IEEE Data Compression Conference, pp. 190-199.
[8] Willems, F., Shtarkov, Y. and Tjalkens, T. (1995) The context-tree weighting method: Basic properties. IEEE Transactions on Information Theory, 41(3):653–664
[9] Rissanen, J. (1983) A universal data compression system. IEEE Transactions on Information Theory, 29(5):656–664
[10] Weinberger, M.J., Lempel, A. and Ziv, J. (1992) A sequential algorithm for the universal coding of finite memory sources. IEEE Transactions on Information Theory, 38(3):1002–1014
[11] Bloom, C. (1996) Solving the Problems of Context Modeling. http://www.cbloom.com/papers
[12] Moffat, A. (1990) Implementing the PPM data compression scheme. IEEE Transactions on Communications, 38(11):1917–1921.
[13] Howard, P. G. (1993) The Design and Analysis of Efficient Lossless Data Compression Systems. PhD thesis, Brown University.
[14] Teahan, W.J. (1995) Probability Estimation for PPM. http://www.cs.waikato.ac.nz/papers/pe_for_ppm
[15] Weinberger, M. J., Seroussi, G. and Sapiro, G. (1995) LOCO-I: a low complexity lossless image compression algorithm. ISO Working Document ISO/IEC JTC1/SC29/WG1 N203.
[16] Shkarin, D. (1999) BMF v.1.1 – lossless image compressor. ftp://ftp.elf.stuba.sk/pub/pc/pack/bmf_1_10.zip
[17] Shkarin, D. (2000) PPMDF – fast PPM compressor for textual data. ftp://ftp.elf.stuba.sk/pub/pc/pack/ppmdf.rar
[18] Info-ZIP Group (1999) Zip v.2.3 - compression and file packaging utility. http://www.cdrom.com/pub/infozip
[19] Seward, J. (2000) BZip2 v.1.0 - block-sorting file compressor. http://www.muraroa.demon.co.uk/
[20] Bloom, C. (1999) PPMZ2 - High Compression Markov Predictive Coder. http://www.cbloom.com/src
[21] Volf, P.A.J. (1996) Text compression methods based on context weighting. Technical report, Stan Ackermans Institute, Eindhoven University of Technology.
[22] Буяновский, Г. (1994) Ассоциативное кодирование. Монитор, 8:10-22.
 На реальных данных ограниченной длины, различие между предсказаниями которые дают PPM и PPM* невелико. На Рис. 1 приведена относительная доля символов, которые могут быть предсказаны контекстами разных порядков в моделях PPM и PPM* для некоторых файлов из Calgary Corpus. Как видно, при выборе порядка модели 6 и выше, число таких символов мало и можно рассматривать модель PPM как весьма точную аппроксимацию модели PPM*. Поведение файла pic противоречит такому предположению, однако на самом деле, этот файл содержит двумерные данные и плохо соответствует парадигме “universal data compression”. В силу этого предположения, мы не будем проводить особо строгих различий между PPM и PPM* и будем применять выводы полученные для контекстно-неограниченной модели к построению реализации контекстно-ограниченной модели и наоборот, применять данные полученные с помощью этой реализации к пониманию поведения PPM*.
На реальных данных ограниченной длины, различие между предсказаниями которые дают PPM и PPM* невелико. На Рис. 1 приведена относительная доля символов, которые могут быть предсказаны контекстами разных порядков в моделях PPM и PPM* для некоторых файлов из Calgary Corpus. Как видно, при выборе порядка модели 6 и выше, число таких символов мало и можно рассматривать модель PPM как весьма точную аппроксимацию модели PPM*. Поведение файла pic противоречит такому предположению, однако на самом деле, этот файл содержит двумерные данные и плохо соответствует парадигме “universal data compression”. В силу этого предположения, мы не будем проводить особо строгих различий между PPM и PPM* и будем применять выводы полученные для контекстно-неограниченной модели к построению реализации контекстно-ограниченной модели и наоборот, применять данные полученные с помощью этой реализации к пониманию поведения PPM*. - сумма значений всех счетчиков частот, esc - специальный символ ухода на модель меньшего порядка,
- сумма значений всех счетчиков частот, esc - специальный символ ухода на модель меньшего порядка, 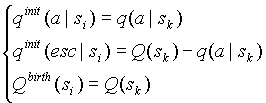 , (2.2-1)
, (2.2-1)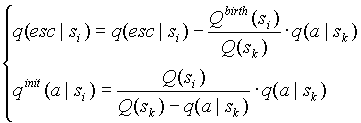 (2.2-2)
(2.2-2)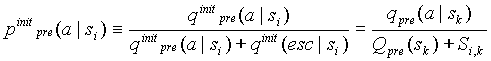 , (2.3-1)
, (2.3-1)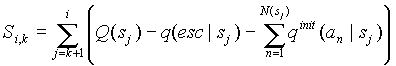 - статистика, накопленная в контекстах
- статистика, накопленная в контекстах 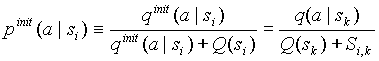 , (2.3-2)
, (2.3-2) 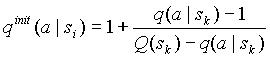 (2.4-1)
(2.4-1)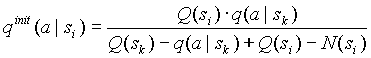 (2.4-2)
(2.4-2)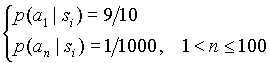 (4.1)
(4.1)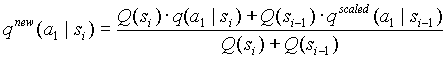 ,
,  .
.